The following publication has been lightly reedited for spelling, grammar, and style to provide better searchability and an improved reading experience. No substantive changes impacting the data, analysis, or conclusions have been made. A PDF of the originally published version is available here.
It is not difficult to come up with a definition of the business cycle that most of us would understand. A thornier issue is how to come up with an empirical measure of the business cycle. This article tackles the question and, in the process, offers a new measure of the U.S. business cycle, derived from regional data. A highlight of this approach is that it facilitates the identification of region-specific influences, such as technology booms or commodity price spikes.
On a recent flight to Australia, the traveler in the neighboring seat (upon learning that I was an economist) promptly asked me to explain what the business cycle was. I pointed out that I was an academic economist and that my answer might be a little vague. My neighbor quickly reminded me that we had 15 hours to work out the details. In fact, as I explain below, my definition of the business cycle is pretty easy to understand, so it took no time at all to answer her question. On the other hand, I did not complete my answer to her follow-up question on whether it was possible to come up with an empirical measure of the business cycle before touching down at Sydney’s Kingsford Smith Airport, since she tended to doze off every time I uttered some statistical jargon.
The mainstream academic view of the business cycle has its roots in the pioneering analysis of Burns and Mitchell conducted in the 1940s.1 Burns and Mitchell’s definition emphasizes that business cycles consist of expansions occurring at about the same time in many economic activities, followed by similarly general contractions.2 In other words, the business cycle is not marked by a large upswing or downturn in a particular industry or economic region, but is the outcome of an upswing or downturn in many industries or regions.3
In this Chicago Fed Letter, I offer a new measure of the U.S. business cycle, derived from regional economic data, that is consistent with the narrower academic definition of the business cycle.4 I focus on the differences and common features of U.S. regional cyclical fluctuations, with common movements across regions measuring the U.S. business cycle and the remaining variation highlighting region-specific sources of disturbance.
Measuring cyclical fluctuations
The starting point for any business cycle analysis is the age-old problem of decomposing fluctuations in economic growth into trend and cyclical components. I use the unobserved components (UC) approach developed by Watson.5 Watson’s approach explicitly assumes that current output (measured as the log of U.S. gross domestic product) depends on its most recent past observation plus some random component and a constant term. The constant term, typically called drift, measures the underlying trend growth rate. That is, in the absence of random fluctuations, trend output grows at a rate equal to the drift term. In contrast, positive random fluctuations lead to trend growth in excess of the drift, while negative random fluctuations cause the trend to grow by less than the drift. Using this method, Watson generated a cyclical component for aggregate U.S. output with peaks and troughs that closely matched those reported by the National Bureau of Economic Research’s (NBER) Business Cycle Dating Committee.
Following Watson’s approach, I assume that log of per capita income for the eight U.S. Bureau of Economic Analysis (BEA) regions is composed of a trend, which is modeled as a random walk with drift and a stationary cyclical component. I build on his approach by assuming that the cyclical component of U.S. regional income is made up of two parts, a common cycle across regions, modeled as a second-order autoregression, and a region-specific cycle, modeled as a first-order autoregression. Following my own research, I also allow the drift to vary over time, with three discrete shifts in the trend growth rate occurring from the start of the sample, 1961:Q1 to 1972:Q2, the productivity slowdown era from 1972:Q3 to 1995:Q4, and the new economy era from 1997:Q1 to the end of the sample, 2001:Q4.6 The resulting common cyclical component is my measure of the U.S. business cycle, while the remaining region-specific components give us some insight into the difference sources of disturbances affecting U.S. economic regions.
U.S. business cycle
Figure 1 plots the common cyclical component of log per capita regional income of the eight BEA regions from 1961:Q1 to 2000:Q4, against the NBER’s peak-to-trough dates. The common cycle generates turning points that match up closely with the NBER’s business cycle dates. According to this measure of the business cycle, the U.S. economy has been operating below its trend for much of the 1990s. However, I estimate the average trend growth rate of per capita income across all regions to be about 1 percentage point higher in the second half of the decade than it was in the productivity slowdown period from the early 1970s to mid-1990s.
1. U.S. business cycles
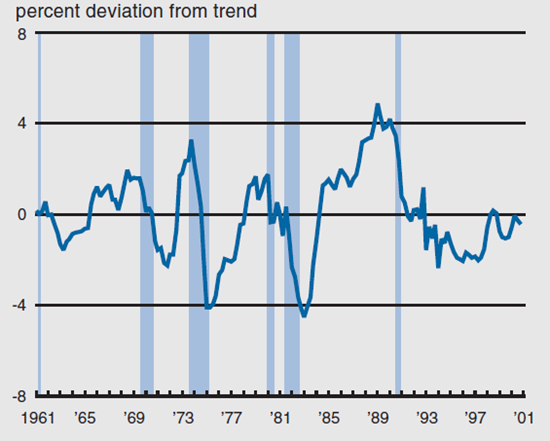
Source: Author’s calculations based on BEA data.
To test whether U.S. regions have different sensitivity to the U.S. business cycle, I allow the regional cyclical component to be a function of the common cyclical component scaled by a sensitivity coefficient. In order to identify these coefficients, I need to set the sensitivity coefficient for one region to be one. I use the Southeast as the benchmark region, largely because the volatility of fluctuations of the quarterly growth rates of Southeast income is the same as that of aggregate U.S. income. (Except for the values of the sensitivity coefficients, all other results reported here are invariant to the choice of benchmark region.) My results indicate that the Plains (coefficient of 1.10) is the only region that is more sensitive than the Southeast. The Great Lakes’ sensitivity to the U.S. business cycle is similar to the Southeast’s, while the other five regions are less sensitive than the Southeast (i.e., coefficients less than one). This suggests that common cyclical fluctuations have a greater impact on the incomes of the Great Lakes, Plains, and Southeast regions, reflecting the fact that a larger share of their income comes from sectors that are more cyclically sensitive, such as agriculture and manufacturing.
Region-specific cycles
There are other elements of regional cyclical fluctuations that are not explained by the scaled common cycle. I plot these region-specific or idiosyncratic business cycles in figure 2. Elsewhere, I have explored whether shocks that originate in one region are subsequently transferred to other regions and find that there is no evidence of statistically significant transmission or spillover of cyclical fluctuations across regions.7 Given the different industry mix and strong interregional trade across U.S. regions, this is evidence against theories of the business cycle that suggest it owes to cyclical fluctuations being transmitted through trade or production linkages. Taken at face value, my finding suggests that the U.S. business cycle is a byproduct of common cyclical shocks that simultaneously affect all regions.
2. Region-specific cycles
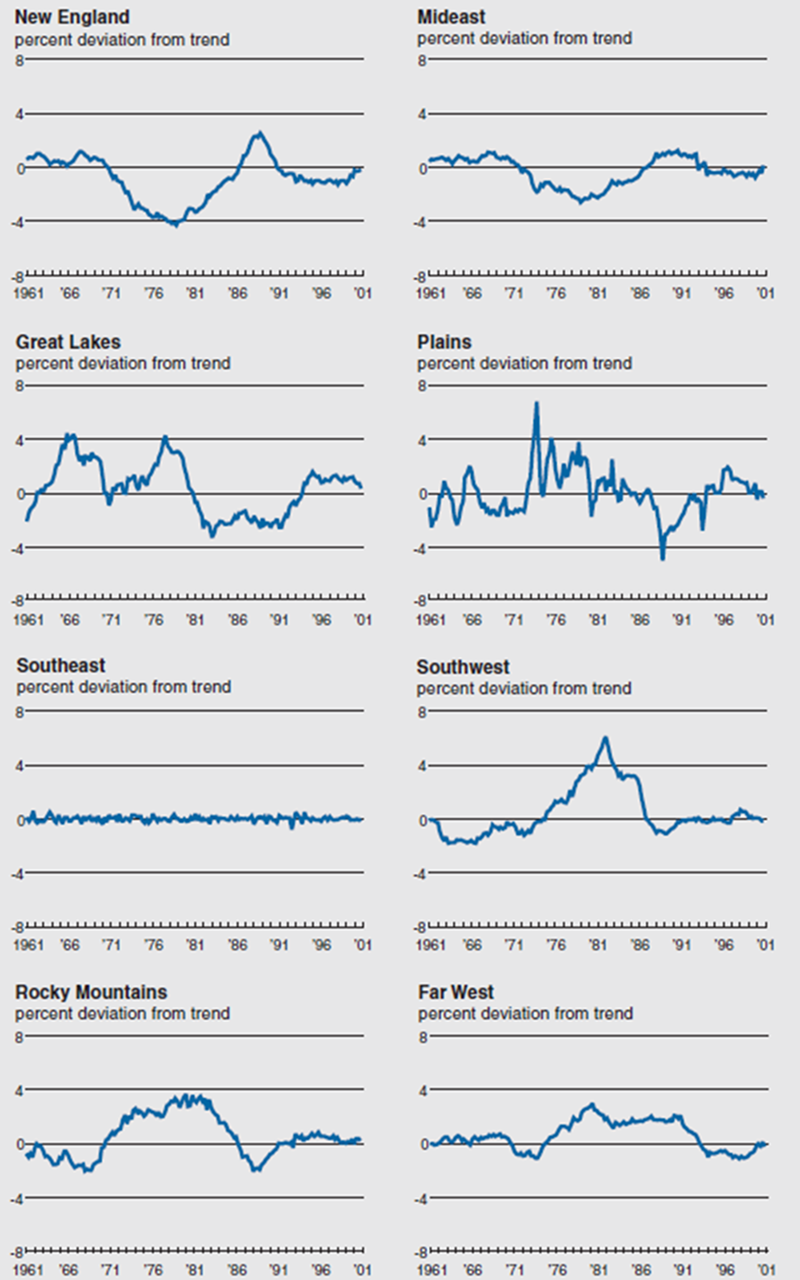
According to figure 2, the Southeast has a very weak region-specific cycle (best described as noise), suggesting that its cyclical behavior is largely explained by fluctuations in the common cyclical component. This reflects the fact that the industrial composition of the Southeast closely matches that of total U.S. income.
In contrast, the Southwest, which derives a disproportionate share of its income from oil production, has a far more persistent idiosyncratic cyclical income component, with fluctuations that are dominated by movements in oil prices. This is most pronounced in the 1970s following the two oil price hikes. Similarly, fluctuations in the mining-intensive Rocky Mountains are influenced by movements in minerals prices. For example, the oil price hikes of the 1970s also raised the prices of oil substitutes, which is reflected by the fact that Rocky Mountain’s income is well above its trend over this period. The Plains is also heavily influenced by commodity price fluctuations. Given the relatively large share of activity that is devoted to agriculture in this region, it is not surprising that the idiosyncratic income component of the Plains takes on the highly volatile pattern of agricultural prices. For instance, the huge commodity price spike that coincided with a worldwide boom in economic activity in 1973 is reflected by the idiosyncratic component of Plains income being 7% above its trend over this period.
Economic activity in the Great Lakes is heavily influenced by developments in durable manufacturing. The best example is the Rust Belt era, which began with a strong regional downturn in late 1970s and ended with a regional recovery in the early 1990s. The general view of why this came about is that the Great Lakes manufacturing sector had developed earlier than that of other industrial regions, so its technology tended to be of an earlier vintage and relatively less efficient. So, in the wake of the oil price shocks, the Great Lakes’ manufacturing sector experienced a relatively larger decline in demand for its products, as a significant share of its market share went to regions with newer (more efficient) plants. It is widely believed that the downturn of the early 1980s drove out a significant share of the older plants with inefficient capital, thereby paving the way for more efficient plants with newer technologies that could fill the growing demand for durable goods when the economy recovered in the early 1990s.8
We observe a different cycle for the formerly industrial regions of New England and the Mideast. New England’s idiosyncratic cycle reflects the high-tech boom that started in the late 1970s, which more than offset the decline in activity bought about by the rapid erosion of the region’s industrial sector in the early 1970s. The so-called Massachusetts economic miracle came to an end in the late 1980s for two reasons. First, rapid technological developments by high-tech industries in other regions dulled the region’s competitive edge and eroded its market share. Second, the end of the Cold War brought about a dramatic decrease in the demand for the region’s defense-related products. The Mideast’s idiosyncratic cycle also reflects the erosion of its industrial sector, which began in the early 1970s. However, in contrast to New England, the Mideast’s turnaround was fueled by growth in demand for its financial services, which has persisted since the mid-1980s. The Far West’s idiosyncratic cycle was influenced by some of the same events that shaped New England’s cycle. For instance, the above-trend income of the mid-1970s coincides with the rapid growth of the computer industry in Silicon Valley. Furthermore, the return to trend income in the early 1990s was fueled by the same cut in defense expenditure that led to the downturn in New England.
Conclusion
Academic economists have emphasized for some time that business cycles consist of persistent expansions occurring at about the same time in many economic activities, followed by similarly persistent general contractions. Using U.S. regional per capita income data, I show how one can apply this definition to get a new statistical measure of the U.S. business cycle, with turning points that closely match those of the NBER’s Business Cycle Dating Committee. Another feature of my approach is that it allows me to decompose regional cyclical fluctuations into common and idiosyncratic components, with the latter serving as a useful tool for analyzing the effects of region-specific influences such as technology booms or commodity price spikes.9
Notes
1 See, A. Burns and W. Mitchell, 1946, Measuring Business Cycles, New York: National Bureau of Economic Research.
2 Burns and Mitchell’s definition of the business cycle also carries the condition that the sequence of changes in activity across many industries/regions be recurrent but not periodic and have duration of 18 months to eight years.
3 The NBER’s Business Cycle Dating Committee emphasizes the economy-wide nature of business cycles in its discussion of the latest business cycle peak, which occurred in March 2001. See “The NBER’s business-cycle dating procedure,” p. 2.
4 In the article, I use regions as defined by the U.S. Bureau of Economic Analysis.
5 M. W. Watson, 1986, “Univariate detrending methods with stochastic trends,” Journal of Monetary Economics, Vol. 18, pp. 49–75.
6 For details, see M. A. Kouparitsas, 1999, “Is there evidence of the New Economy in the data,” Federal Reserve Bank of Chicago, working paper.
7 For details, see M. A. Kouparitsas, 2002, “Understanding U.S. regional business cycles: How important are spillovers and common shocks?” Federal Reserve Bank of Chicago, Economic Perspectives, Fourth Quarter, forthcoming.
8 For an extended discussion of the Great Lakes recovery, see W. A. Testa, T. H. Klier, and R. H. Mattoon, 1997, “Assessing the Midwest economy: Looking back for the future,” Federal Reserve Bank of Chicago.
9 See, for example, M. A. Kouparitsas, 2001, “Is the United States an optimum currency area? An empirical analysis of regional business cycles,” Federal Reserve Bank of Chicago, working paper, for a discussion of the common and idiosyncratic responses of U.S. regions to U.S. monetary policy.










