Introduction and summary
Central banks around the globe are commonly charged with the responsibility of producing timely predictions of the current state of the economy in the course of conducting monetary policy. This task is often difficult given the substantial publication lags in comprehensive measures of economic activity, such as U.S. real gross domestic product (GDP). Accordingly, a large literature has developed methods that utilize the broad set of available high-frequency (typically monthly) economic indicators to track changes in economic activity in real time. In this article, we employ recent advances in this literature to produce a new “big data” index of U.S. economic activity that can be used to track U.S. business and inflation cycles in real time and estimate monthly real GDP growth.
Our work in this area is an extension of the nearly 20-year tradition established by the Chicago Fed National Activity Index (CFNAI). The CFNAI is a monthly measure of growth in U.S. economic activity constructed from a panel of 85 macroeconomic time series encompassing four types, or groups, of indicators: production and income; employment, unemployment, and hours; personal consumption and housing; and sales, orders, and inventories.1 By including such a diverse set of indicators, the index is designed to capture broad movements in aggregate U.S. economic activity around a long-term historical rate of economic growth. A zero value of the index indicates that growth in economic activity is proceeding along at this rate, while a negative value indicates below-average growth and a positive value indicates above-average growth. In what follows, we present a new estimation methodology for economic activity indexes that allows us to efficiently use a significantly broader set of macroeconomic indicators than the CFNAI and more accurately track U.S. economic activity around its long-run growth trend.
The CFNAI is estimated as the first principal component of its constituent time series. As such, it is effectively a weighted average of these series, with their individual weights representing the relative degree to which each series explains the overall variation among all the series. Principal components analysis (PCA) is a common data dimension reduction technique used to summarize the most prevalent aspects of large data sets, typically for the purpose of prediction.2 Hence, it is not surprising then that many of the applications of the CFNAI have focused on the forecasting of U.S. inflation and real GDP growth (Brave and Butters, 2010, 2014). Our new activity index instead uses collapsed dynamic factor analysis techniques (Bräuning and Koopman, 2014), which offer a practical compromise between PCA and more recently developed dynamic factor methods that aim to separately make use of both the static and dynamic correlations present in large panels of time series in order to improve prediction.
We view our new index as a big data application in macroeconomics (for example, Bok et al., 2017). Broadly speaking, big data techniques attempt to address the “curse of dimensionality,” or the fact that the number of parameters to be estimated increases as the number of variables included in a model increases. In general, there are two approaches to this problem: dense or sparse modeling (Giannone, Lenza, and Primiceri, 2018). The estimation methodology that we present here for our new economic activity index closely follows the spirit of dense modeling by aiming to extract as much information on the overall state of the economy as efficiently as possible while using all of the available data. This stands in contrast to a sparse modeling approach, which instead seeks to identify a subset of indicators with the most predictive power for the overall state of the economy and exclude those deemed less important. In principle, the dense approach acknowledges that all of the economic indicators might be important for measuring the overall state of the economy, despite each indicator’s influence potentially being small.
While the size of our data set is substantially smaller than typical big data applications, efficiently utilizing our large panel of macroeconomic time series does still require that novel alterations be made to standard data dimension reduction tools, such as PCA. Our new index summarizes the information in an unbalanced3 panel of 500 U.S. macroeconomic time series extending back to 1960—roughly six times more than the CFNAI with an additional seven years of historical coverage. These 500 time series broadly reflect the set of real economic activity indicators commonly used to forecast U.S. GDP. In addition, the new index uses mixed-frequency state-space modeling techniques that benchmark it directly to U.S. real GDP growth. This occurs as the estimation of trend GDP growth takes place within the model itself, whereby we link the new index directly to the cyclical component of a trend–cycle decomposition of GDP growth at a monthly frequency. A useful byproduct of this process is a new estimate of monthly real GDP growth.
The CFNAI was originally designed as a leading indicator for inflation (Stock and Watson, 1999). Large positive values of the index have been shown to be associated with sustained increasing inflation (Fisher, 2000). However, much of the CFNAI’s value derives instead from its ability to capture the timing of U.S. business cycles, or the periodic fluctuations in economic activity around its long-term trend (Evans, Liu, and Pham-Kanter, 2002). The CFNAI has been shown to align with U.S. expansions and recessions according to the National Bureau of Economic Research (NBER) with close to 95 percent accuracy (Berge and Jordà, 2011). This very strong performance in detecting business cycles can also be seen in related higher-frequency measures capturing U.S. business conditions constructed using similar methodologies, such as the daily Aruoba-Diebold-Scotti Business Conditions Index (ADS index) produced by the Federal Reserve Bank of Philadelphia (Aruoba, Diebold, and Scotti, 2009).
Relying on the precedents set by the CFNAI and related alternatives, we evaluate how well our new index estimation methodology performs in identifying U.S. business and inflation cycles. For instance, we show that our new activity index aligns with historical U.S. business cycles with 99 percent accuracy, outperforming both the CFNAI and the ADS index with statistical significance. In addition, we isolate a leading component of the new index exhibiting predictive power for business cycle fluctuations that is roughly on par with that of the Conference Board Leading Economic Index for the U.S.—a closely followed composite index intended to forecast future U.S. economic activity. This component of our new index is also shown to be superior at identifying cycles in U.S. inflation in comparison with the CFNAI.
In the next section, we detail our new estimation methodology and compare it with leading alternatives. Next, we describe our expanded data set, compare estimates of our new index and the CFNAI, and describe our estimate of monthly real GDP growth. Finally, we evaluate the ability of our new index to capture the historical timing of U.S. business and inflation cycles, and then compute thresholds for the new index and one of its components that can be used in real time to signal turning points in both cycles.
A new estimation methodology for activity indexes
The number of data dimension reduction techniques available to researchers wishing to summarize large data sets is rapidly expanding with the growth of big data applications. Within the subset of linear estimators commonly used for data dimension reduction, principal components analysis is attractive for a number of reasons when dealing with large panels of macroeconomic time series. PCA applies an objective criterion to the estimation of an index like the CFNAI—which seeks to identify the single common component responsible for the most variation within and across the index’s constituent time series. Under a minimal set of assumptions, PCA has been shown to provide consistent estimates of such latent common factors (Bai and Ng, 2002) even in the presence of missing or incomplete data (Stock and Watson, 2002a, 2002b). The factors are then typically used to forecast macroeconomic aggregates such as GDP (Stock and Watson, 2002a, 2002b; and Giannone, Reichlin, and Small, 2008).
Another advantage of PCA is that it produces estimates of the factors that are intuitively appealing. For example, an index like the CFNAI is a weighted average of its constituent time series, where the weights reflect the importance of each individual series in explaining the total variation among all the series. Recent work in this area has sought to improve upon the precision of PCA either by building into the objective criterion restrictions suggested by economic theory (Reis and Watson, 2010) or by introducing into the objective criterion dynamic elements that offer additional cross-sectional and time-series averaging advantages (Stock and Watson, 2011). By far, the most popular of these alternative methods is dynamic factor analysis—which, given separate data-generating processes for the panel of time series and its latent common factors, seeks to maximize their joint likelihood.
Box 1 summarizes the main aspects of how these alternative estimation methods differ from PCA. One potential drawback of using several of these alternatives is their computational cost. With a fixed number of common factors in a typical dynamic factor analysis, for each additional time series the number of parameters required to be estimated by maximum likelihood increases by two (for example, an additional factor loading and idiosyncratic variance—see box 1 for further details). This is in contrast to PCA, where it increases by one (that is, only an additional factor loading must be estimated because all idiosyncratic variance terms are assumed to be equal—again, see box 1 for further details). Efficient expectation-maximization (EM) algorithms have been developed to estimate dynamic factor models using large panels of time series (Doz, Giannone, and Reichlin, 2012)—even models with unbalanced panels such as ours (Bańbura and Modugno, 2014); but given the size of our panel of time series, the computational burden of these estimation methods remains problematic.
Another drawback of the traditional dynamic factor model approach involves the potential concern associated with the presence of “weak” common factors in the panel (Chudik, Pesaran, and Tosetti, 2011).4 The presence of weak factors violates the necessary assumptions for the identification of the approximate factor model underlying both PCA and factor analysis.5 In other words, it might be a disadvantage to use data from a large data set of economic indicators to measure the state of the overall economy if enough of these indicators display sectoral co-movements distinct from the overall economy. The CFNAI’s data set and the new expanded data set discussed here are highly likely to fall subject to these concerns given the prevalence of both top-line and underlying sectoral and geographic time series that are included in both panels. Thus, what would be appealing for such a data set is an approach that offers the advantages of data dimension reduction without the unwanted side effect of potentially confounding idiosyncratic co-movements among groups of indicators with variation that is common to all of them.
In our view, collapsed dynamic factor analysis (Bräuning and Koopman, 2014) is precisely that approach overcoming these shortcomings of PCA and traditional dynamic factor methods. In many respects, collapsed dynamic factor analysis instead resembles another popular alternative to PCA called partial least squares, or PLS (Exterkate et al., 2013; and Groen and Kapetanios, 2016). While PCA reduces the variation among all the time series into a component that explains the most of all their variation, PLS can be thought of as reducing the variation among the series down to a common component that is the most closely related to a prespecified “target” variable. Collapsed dynamic factor analysis aims to achieve something similar to PLS, but within the more traditional dynamic factor framework.
Fortuitously, the incorporation of an appropriately prespecified target variable can also serve as an “instrument”6 to eliminate the unwanted side effect the presence of weak factors would have when using PCA to estimate the index. This process works in a similar fashion to the standard errors-in-variables framework used to address mismeasured data (Bräuning and Koopman, 2014). Additionally, the “collapse” of the panel of time series down to a dimension of size equal to the number of common factors greatly reduces the number of parameters to be estimated by maximum likelihood compared with traditional dynamic factor analysis. For instance, the maximum likelihood estimation for our new index is reduced to fewer than ten parameters, versus over 1,000 using traditional dynamic factor methods. These advantages do not come without a cost, however, in that they require a priori knowledge of an appropriate target variable.
Since we are interested in aggregate economic activity, we collapse our new data set using U.S. real GDP growth as our instrument. However, in order to use quarterly real GDP growth as a target variable for our monthly economic activity index, we must first specify a mixed-frequency trend–cycle decomposition of it, with the cyclical component corresponding to the new monthly index. Underlying the mixed-frequency estimation process are parameter restrictions, called “accumulators,” requiring the cyclical component of quarterly real GDP growth to be based on the appropriately aggregated monthly activity index. These restrictions act as linear constraints on the estimation of the model in order to preserve the temporal aggregation relationships between the panel of monthly time series, their common factor, and quarterly real GDP growth. Box 2 details the full process used to arrive at our new index.
By benchmarking our new activity index directly to U.S. real GDP growth, we can also present it in natural as opposed to standard deviation units, with movements in the index corresponding to percentage point deviations from trend real GDP growth. We can do this because the estimation of trend real GDP growth now occurs simultaneously with the activity index. A useful byproduct of this process is a new estimate of monthly real GDP growth (Mitchell, 2014). Beyond the statistical advantages offered by this approach, it also has a basis in structural models that incorporate sectoral linkages (Brave, Butters, and Kelley, 2019). In these terms, we view our new estimation methodology for activity indexes as being broadly in line with the history of semistructural U.S. business cycle measurement that grew out of the initial work of Sargent and Sims (1977) and Geweke (1977).
Data for the new index
We estimate our collapsed dynamic factor model for our new activity index using data on quarterly U.S. real GDP growth and a panel of 500 monthly time series of U.S. real economic activity since January 1960.7 To arrive at our set of monthly indicators, we started with the 85 indicators used in the CFNAI.8 Many of these same time series can also be found among those used in the Conference Board’s Coincident, Leading, and Lagging Economic Indexes for the U.S., as well as in other prominent U.S. business conditions indexes, such as the ADS index. To this list, we then added any additional monthly real activity time series used by the Conference Board, as well as those found in the databases of the St. Louis Fed’s FRED-MD (McCracken and Ng, 2016), the Atlanta Fed’s GDPNow (Higgins, 2014), and the New York Fed Staff Nowcast model (Bok et al., 2017). Finally, we arrived at our full set of monthly time series by filling in geographic and sectoral details wherever possible using various Haver Analytics databases.
In expanding the data set for our new index relative to that for the CFNAI, we emphasized broadening coverage of government spending, international trade, personal consumption, and residential and nonresidential investment. A common criticism of the CFNAI is that it places too much importance on the manufacturing sector. This criticism stems from the fact that time series for the manufacturing sector tend to have longer histories than those for the nonmanufacturing sector, thus making the former easier to incorporate into indexes like the CFNAI. Our new estimation methodology, however, lessens the need for us to rely solely on time series with long histories, allowing us to use an unbalanced panel of indicators (see note 3). Eliminating the need for a balanced panel of time series opens up the possibility of using a much larger set of indicators, including several from the nonmanufacturing sector of the U.S. economy. A full list of indicators with sources and transformations can be found in table A1 of the separate appendix (see note 7).
Comparing the new index and CFNAI
Figure 1 contains a plot of our new activity index and the CFNAI. The new index starts in January 1960, while the CFNAI begins in March 1967. For the purpose of comparison, both indexes are presented in standard deviation units from their historical averages. While both the new index and CFNAI display similar time-series properties, it is readily apparent that the new index is much smoother. In the past, the focus has been given to a three-month moving average of the CFNAI (the CFNAI-MA3), which smooths the volatility in the monthly data while more accurately identifying turning points in U.S. business cycles and periods of sustained increasing inflation than the monthly version. The enhanced cross-sectional averaging afforded by the larger panel of time series and the time-series averaging of our collapsed dynamic factor model instead serve this purpose for our new index.9
Figure 1. New activity index versus CFNAI
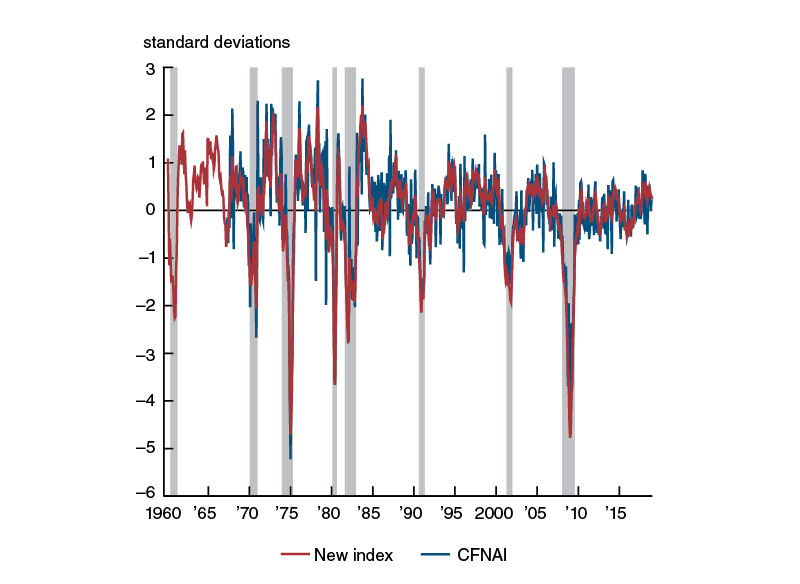
Source: Authors' calculations based on data from Haver Analytics.
The new index and the CFNAI are again presented in figure 2, with the colored areas representing the additive contributions from each of the four categories of indicators currently used to describe the CFNAI—namely, production and income; employment, unemployment, and hours; personal consumption and housing; and sales, orders, and inventories. Decomposing the indexes in this way provides useful information about the main drivers of the U.S. business cycle and highlights subtle differences in their behavior over the cycle (Brave, 2009). In this regard, both the new index and CFNAI are quite similar—with production and income indicators accounting for the largest share of both (34 percent and 36 percent, respectively), followed by employment, unemployment, and hours (23 percent and 32 percent) and then personal consumption and housing (18 percent and 13 percent) and sales, orders, and inventories (14 percent and 19 percent). The new index is also partially determined by quarterly real GDP growth (accounting for 12 percent of the index).10
Figure 2. Contributions to the new activity index and CFNAI
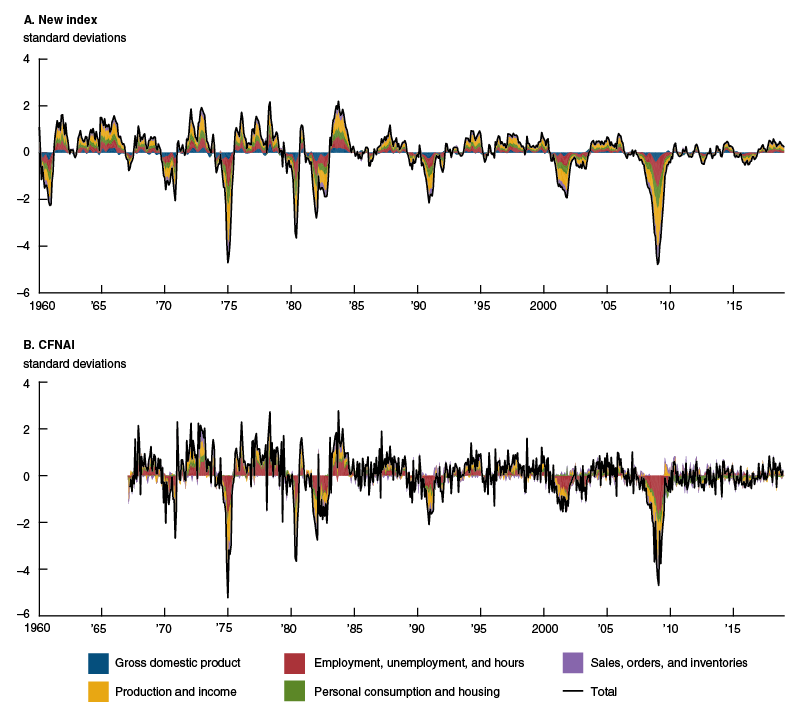
Source: Authors’ calculations based on data from Haver Analytics.
Figure 3 presents an alternative way of capturing the information in both indexes. It relies on the concept of a diffusion index, where each point in time of the new index and CFNAI is reexpressed as the sum of the weights given to all positive contributors in the index minus the sum of the weights of all negative contributors (Brave and Lichtenstein, 2012).11 A diffusion index of this type is one way in which to capture the “momentum” behind recent changes in the index, given that changes in the index driven by a large percentage of indicators pushing in the same direction tend to be more persistent than those driven by a small number of indicators. Because it smooths out fluctuations over time, the three-month moving average of the resulting diffusion index for the CFNAI is given focus. Our mixed-frequency dynamic factor model suggests an alternative construction, whereby we temporally aggregate the diffusion index into a “triangle average” in order to match the temporal aggregation properties of quarterly real GDP growth in the model (see box 2 for further details). The resulting diffusion index is again much smoother, and it captures business cycle turning points in a similar fashion as the CFNAI Diffusion Index.
Figure 3. New diffusion index versus CFNAI Diffusion Index
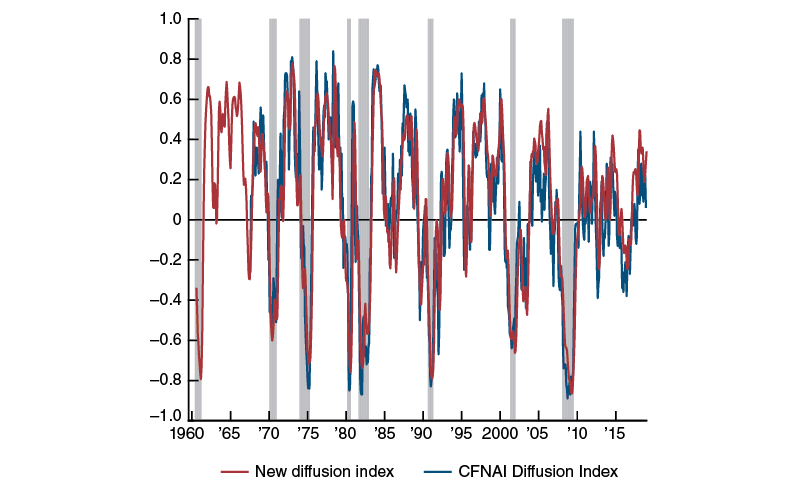
Source: Authors’ calculations based on data from Haver Analytics.
An appealing feature of the new index versus the CFNAI is that we can also present the new index in the same units as quarterly annualized U.S. real GDP growth. In addition, we can also decompose it along the lines of the more traditional national income and product accounts (NIPA) methodology—that is, it can be broken down by contributions from consumption, investment, government spending, and net exports categories (which sum to real GDP). Figure 4 depicts this alternative way of expressing the new index by NIPA conventions. The colored areas in this figure represent the contributions of the monthly indicators to the new index separated into three categories: 1) consumption, 2) investment, and 3) other. The final category represents the sum of the contributions of government spending and net exports indicators, along with quarterly real GDP growth. When the index is broken down this way, one can readily see the contributions of consumption and investment indicators dominate the index, just as employment- and production-related indicators do in figure 2.
Figure 4. New activity index, by NIPA category of indicators
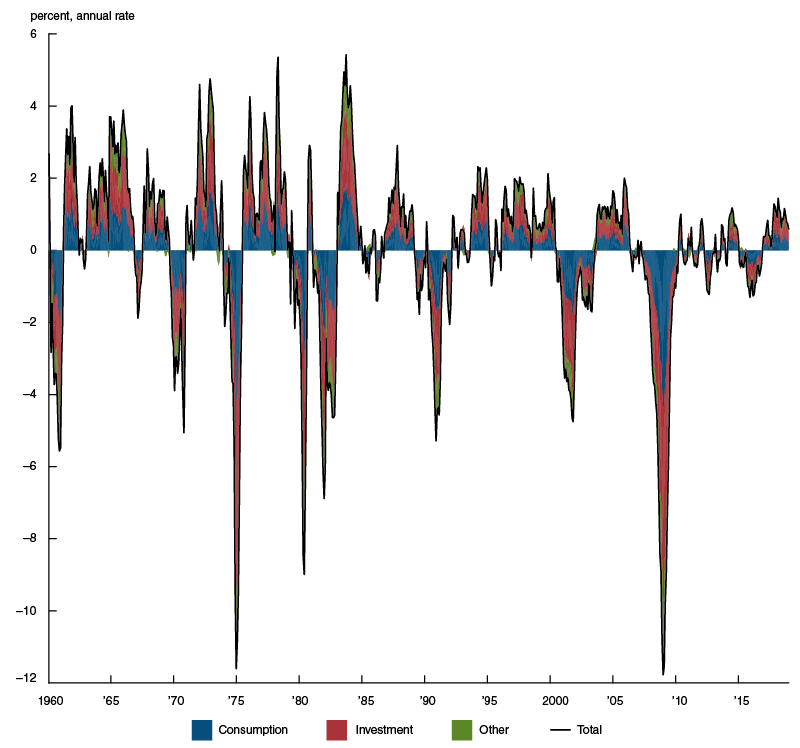
Source: Authors’ calculations based on data from Haver Analytics.
We can also go one step further and provide an estimate of monthly real GDP growth in similar annualized units. Such a measure results directly from our trend–cycle decomposition of quarterly real GDP growth in our collapsed dynamic factor model. For this reason, we can also estimate trend monthly real GDP growth in order to provide a direct measure of the trend growth rate around which the new index is benchmarked. Figure 5 contains both of these estimates, along with quarterly annualized real GDP growth from the U.S. Bureau of Economic Analysis. In keeping with what we have found in past work, trend monthly real GDP growth is shown to have slowly declined over time since 1960 (Brave and Butters, 2013, 2014). Based on data available in late January 2019, our estimates suggest that trend growth is currently around 2.3 percent.
Figure 5. U.S. real GDP growth
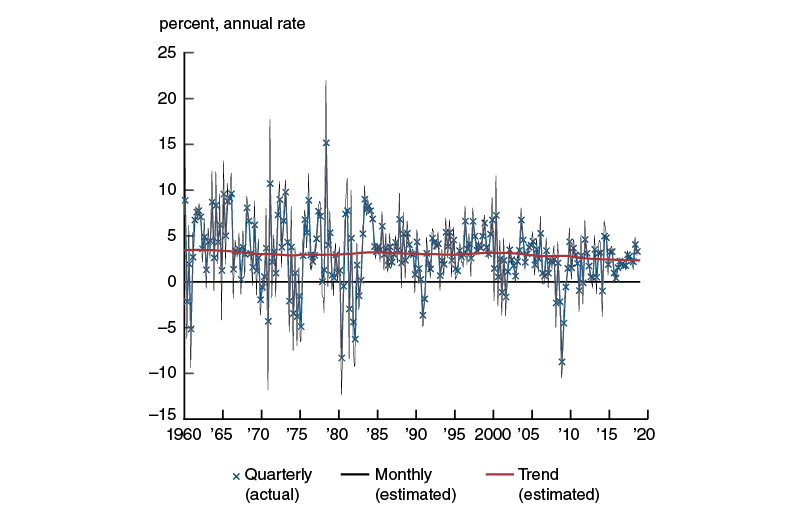
Source: Authors’ calculations based on data from Haver Analytics.
Business and inflation cycles
We now take a closer look at the ability of the new activity index to capture U.S. business cycles. To do so, we rely on a nonparametric technique described in box 3 for judging the ability of an index to separate the expansionary and recessionary phases of the business cycle called receiver operating characteristic (ROC) analysis. This method assigns a score, or an area under the curve (AUC) value, to each index based on its ability to correctly classify U.S. recessions and expansions as a percentage of the observations of an index. For an ideal business cycle indicator, there would not be any values that are consistent with both an expansion and recession. Such an indicator would receive a score of 1, reflecting 100 percent accuracy in identifying periods of expansion and recession. For a random indicator, on average, every value of the index would be just as likely to appear during a recession or expansion, and its score would be 0.5, reflecting that it is likely to be accurate 50 percent of the time in distinguishing expansions from recessions.12 The CFNAI has been shown to be 94.8 percent accurate in identifying expansions and recessions, and the ADS index has demonstrated a 98.6 percent accuracy; these two indexes are gold standards—they perform much better in this regard than a large number of alternative business cycle indicators (Berge and Jordà, 2011). These AUC values imply that roughly 5 percent of the CFNAI’s realizations and 1.5 percent of the ADS index’s are consistent with both a recession and expansion classification.
Figure 6 plots the new activity index versus the ADS index and CFNAI-MA3 over their respective histories, with shaded periods in each panel corresponding to NBER recessions for the United States. We use all available data through late January 2019 for all three indexes and evaluate their historical, or in-sample, fit for U.S. business cycles, as shown in figure 6.13 The new activity index exceeds the historical performance of both the CFNAI-MA3 and the ADS index, registering 99 percent accuracy that is statistically significantly better than both alternative indexes at the 5 percent and 15 percent levels, respectively. This implies that less than 1 percent of months in our sample since January 1960 are classified incorrectly by the new index; in other words, the intersection of the distribution of the new index’s values during months of expansion and during months of recession represents less than 1 percent of its sample history.
Figure 6. Comparison of U.S. economic activity indexes
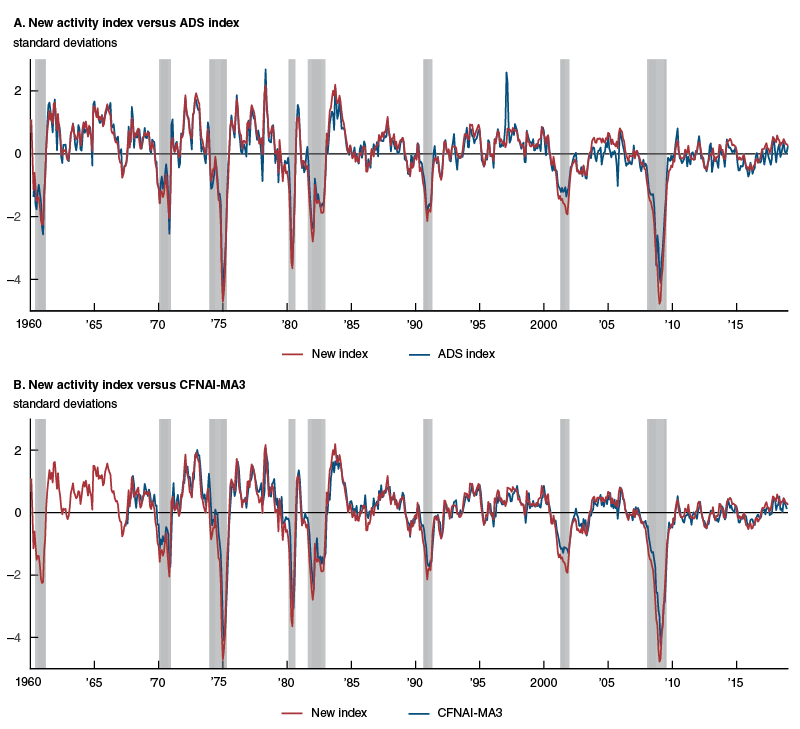
Source: Authors’ calculations based on data from Haver Analytics.
To see this more clearly, view panel A of figure 7, which plots the new index again in standard deviation units with NBER recession shading and “optimal” thresholds as defined in box 3. These thresholds are based on a decision-theoretic use of ROC analysis, which seeks to achieve a prespecified balance between the likelihood of type I (false positive) and type II (false negative) classification errors for the state of the U.S. business cycle. These values are noted in the figure by red dashed horizontal lines. The lower of the two thresholds (–1) denotes the level at which the new index is equally likely to produce a false positive or false negative signal for a recession whenever a reading of the index falls below or moves above it. While tracking the new index relative to this lower threshold, it is easy to see that it does quite well at avoiding both false positives and false negatives apart from a slightly early signal for the 2001 recession and delayed signal for the 1973–75 recession. The higher threshold in the figure (–0.1) corresponds with the level of the index that eliminates all false negative signals, essentially by encompassing the highest reading of the index during the 1973–75 recession.14
Figure 7. U.S. business cycle threshold values
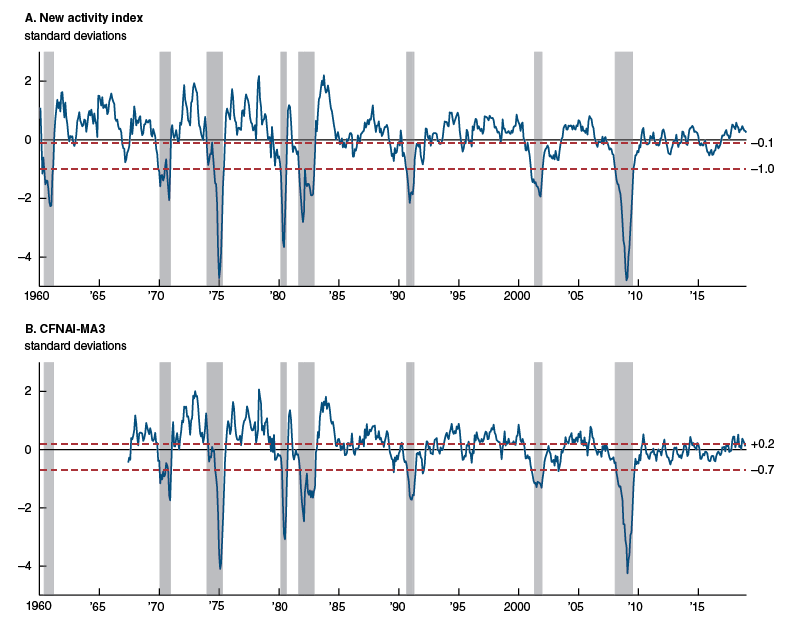
Source: Authors’ calculations based on data from Haver Analytics.
These decision-theoretic thresholds closely resemble the “rules of thumb” that have been used to signal turning points in the business cycle with the CFNAI-MA3; panel B of figure 7 displays these values. In relation to their respective indexes, both sets of thresholds accomplish very similar purposes. In fact, as noted in Brave and Butters (2010), the –0.7 threshold value for the CFNAI-MA3 used to indicate an increasing likelihood of a recession is almost identical to the optimal threshold for this index that balances a desire to avoid false positives with a desire to avoid false negatives. Similarly, the +0.2 threshold for the CFNAI-MA3 used to indicate a significant likelihood of a recovery from a recession serves a similar purpose to the optimal ROC threshold that eliminates all false negatives for this index.
So, what accounts for the performance gains in business cycle timing of the new index over the ADS index and CFNAI-MA3? To determine this, we next use our collapsed dynamic factor model to break down monthly real GDP growth in figure 8 into its trend $\left({{\unicode{x03B1}}_{t}}\right)$ and irregular $\left( {{\unicode{x03B7} }_{t}} \right)$ components (panel B of figure 8), as well as its two underlying business cycle components forming the new activity index—namely, factors ${{\unicode{x03BC} }_{t}}$ and ${{f}_{t}}$ (panel A of figure 8). The trend and irregular components have AUC values very close to 0.5, suggesting that they are equally likely to misclassify both phases of the business cycle; hence, neither component is cyclical in nature. Instead, it is the combination of only the two business cycle components that leads to a 0.99 AUC value for the new index. Interestingly, this occurs despite the fact that both factors ${{\unicode{x03BC} }_{t}}$ and ${{f}_{t}}$ have lower AUC values on their own—specifically, 0.66 and 0.97, respectively.
Figure 8. Components of monthly U.S. real GDP growth
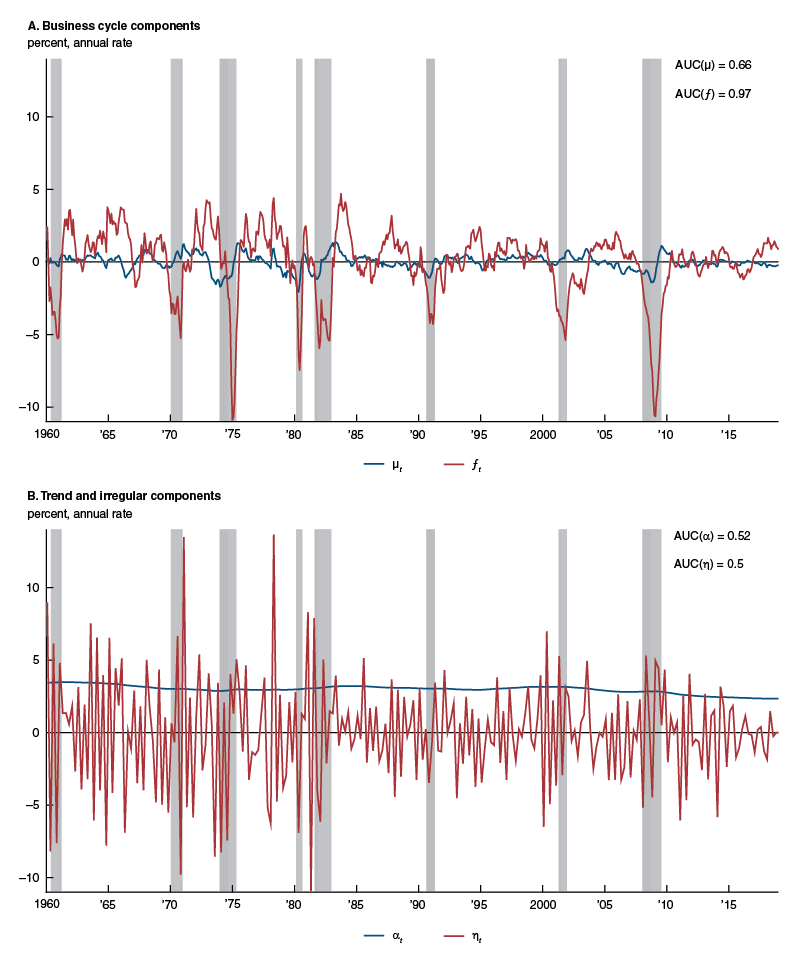
Source: Authors’ calculations based on data from Haver Analytics.
To see why this is the case, view figure 9. This figure plots AUC values for the new index and its two components at both leads and lags (of up to 12 months) of the business cycle. For comparison, it also plots the AUC values of the Conference Board’s Coincident, Leading, and Lagging Economic Indexes for the U.S. The new index is clearly a coincident indicator, given that its AUC values in panel A of figure 9 peak at zero. Furthermore, its AUC values at leads and lags of the business cycle highly resemble those of the Conference Board Coincident Economic Index for the U.S., albeit with statistically significantly higher accuracy contemporaneously (0.99 versus 0.93) and at almost all leads and lags in the panel. In contrast, the component of the new index with a lower contemporaneous AUC value $\left( {{\unicode{x03BC} }_{t}} \right)$ displays a noticeable lead (leftward shift) in its AUC values in panel B of figure 9, suggesting much higher accuracy at leads over the cycle. This pattern closely resembles that of the AUC values at leads over the cycle for the Conference Board Leading Economic Index for the U.S. The component of the new index with a higher contemporaneous AUC value $\left( {{f}_{t}} \right)$, shown in panel C of figure 9, instead displays a very slight lag (rightward shift) in its AUC values, suggestive of a slight lag over the cycle, but much less so than for the AUC values for the Conference Board Lagging Economic Index for the U.S., also depicted in figure 9, panel C.15
Figure 9. AUC values at leads and lags of the U.S. business cycle
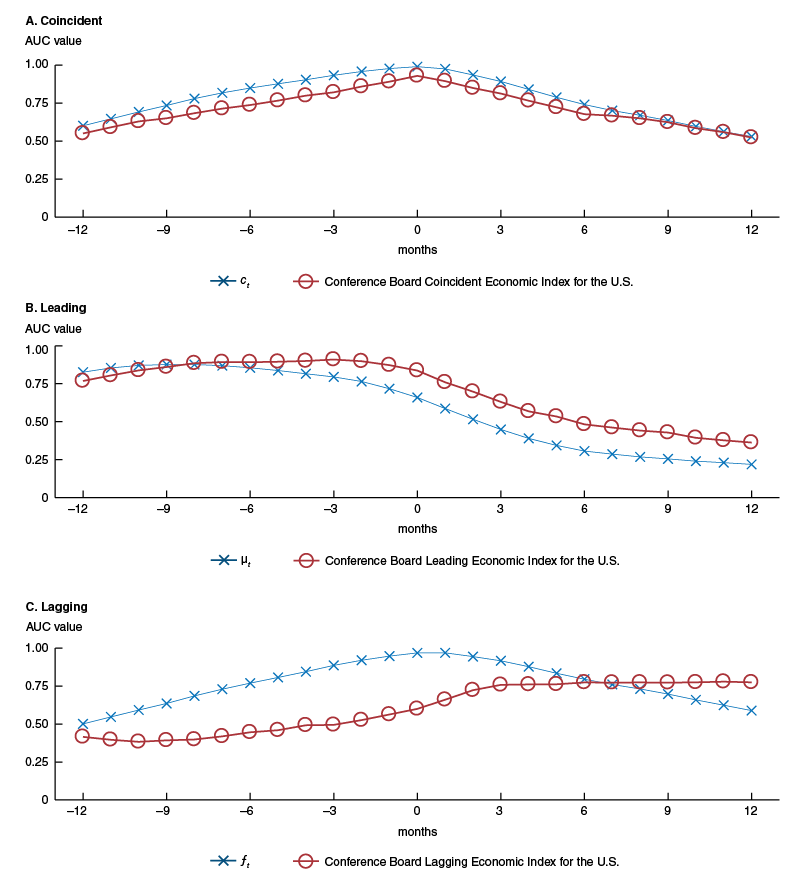
Source: Authors’ calculations based on data from Haver Analytics.
It is, therefore, the combined signal of a slightly lagging component and a highly leading component that produces an AUC value superior to those of both the CFNAI-MA3 and ADS index. It is clear from panel A of figure 8 that the slightly lagging component dominates the new activity index, but the highly leading component does just enough to shape its behavior ahead of business cycle turning points to make a notable difference in its contemporaneous and leading AUC values. If we further combine both of these components with the trend and irregular components in panel B of figure 8 to arrive at our full estimate of monthly real GDP growth, we obtain a much lower AUC value of 0.86. This further demonstrates the value of our trend–cycle decomposition of real GDP growth.
We can also test the ability of the new index to improve upon the performance of the CFNAI as a leading indicator for U.S. inflation. First, we must come up with a set of cycles for inflation similar to the NBER business cycles in order to apply ROC analysis. To do so, we rely on an algorithm used for the CFNAI-MA3 to identify episodes of sustained increasing inflation, as described in box 4. This algorithm produces the set of dates represented as shaded periods in figure 10. With these dates, we apply ROC analysis using values of the new index from 12 months before to assign it a score for identifying U.S. inflation cycles.
Figure 10. U.S. inflation cycle threshold values

Source: Authors’ calculations based on data from Haver Analytics.
The new activity index has an AUC value of 0.6 for identifying U.S. inflation cycles. We compare the performances of the index’s two components with that of the index itself, and again find some differences. This time the index’s components each outperform the index, with the leading component for the business cycle $\left( {{\unicode{x03BC} }_{t}} \right)$ registering an AUC value of 0.7 and the slightly lagging component for the business cycle $\left( {{f}_{t}} \right)$ having an AUC value of 0.67. Notably, the latter’s AUC value is identical to that of the CFNAI-MA3. This result further suggests that, even though it forms a small part of our estimate of monthly real GDP growth, the leading component of the new index $\left( {{\unicode{x03BC} }_{t}} \right)$ has outsized value. Adding the trend component $\left( {{\text{ }\!\!\unicode{x03B1}\!\!\text{ }}_{t}} \right)$ and irregular component $\left( {{\unicode{x03B7} }_{t}} \right)$ of monthly real GDP growth to the new index produces an AUC value of 0.5, suggesting that neither is particularly relevant for identifying inflation cycles (or for identifying business cycles, as shown before).
We can also replicate the threshold values used with the CFNAI-MA3 for signaling turning points in the inflation cycle shown in panel B of figure 10. These thresholds signal an increasing (+0.7) or substantial (+1.0) likelihood of a period of sustained increasing inflation over the coming year. To arrive at similar values for the leading component of the new index in panel A of figure 10, we again use the ROC techniques described in box 3. However, instead of looking to equally balance false positives and false negatives, here we assign a relative weight to each that mirrors the choice of threshold values made in Fisher (2000).16 The thresholds for the leading component of the new index $\left( {{\unicode{x03BC} }_{t}} \right)$ are +0.3 and +1.6. Given these thresholds, this leading component suggests rising inflationary pressures over the coming year at a much lower level of above-trend growth than the CFNAI-MA3; however, the range between increasing and substantial likelihoods of a future period of sustained increasing inflation is significantly wider.17
Conclusion
Our new methodology for economic activity indexes relies heavily on recent advances in dynamic factor analysis that have enabled the use of very large panels of macroeconomic time series, all the while still addressing potential concerns about the consistent estimation of their common factors. The new index that we develop uses over 500 macroeconomic time series and is 99 percent accurate in aligning with historical U.S. business cycles—a statistically significant improvement over common alternatives such as the CFNAI and ADS index. In addition, the new methodology allows us to isolate a leading component of the new index that correlates strongly with the Conference Board Leading Economic Index for the U.S. This leading component also more accurately signals turning points in U.S. inflation over the next 12 months compared with the CFNAI. Finally, our new methodology produces an estimate of monthly real GDP growth and its trend. We plan to update our estimates of monthly real GDP growth and its components at the same time as we update the CFNAI and make our results publicly available online.
NOTES
1 Additional background information on the CFNAI is available online.
2 See the next section, which explains a new estimation methodology for activity indexes, and box 1 for details on principal components analysis.
3 In this context, the term “unbalanced” means that not every time series is of the same length; hence, some time periods will be missing values in the panel.
4 A “weak” common factor in this setting loosely refers to the presence of idiosyncratic cross-sectional correlation that cannot be expected to “cancel out” as the number of time series in the panel increases.
5 For more information on the approximate factor model, see Chamberlain and Rothschild (1983).
6 By “instrument,” we refer to the example of an instrumental variable in the linear regression context. Akin to the use of an instrumental variable in that context, our target variable should satisfy two conditions: 1) It should be informative of the common factor (a relevance condition), and 2) any of its own idiosyncratic variation should be unrelated to the “weak” factors (an exogeneity condition).
7 The estimation sample is padded with two additional quarters (latter half of 1959) of real GDP growth to aid in the identification of the model’s nonstationary trend component. The complete list of 500 indicators, their associated categories, and their respective transformations in the new activity index is shown in table A1 of the separate appendix, available online.
8 A complete list of the 85 indicators, their associated categories, and their respective weights in the current CFNAI is available online.
9 The new index shown in figure 1 and subsequent figures is obtained using the two-sided Kalman smoother that allows estimates of latent variables to be informed by the full history of the observed data.
10 The categories’ and real GDP’s shares accounting for the new activity index do not total to 100 percent because of rounding.
11 The weights referenced here correspond to the factor model’s loadings capturing the sensitivity of each individual time series to movements in the common factor, or index.
12 To provide further intuition for what these scores capture, consider the following thought experiment. Construct a histogram of all the values of a monthly indicator observed during the months of expansion. Then, juxtapose another histogram for the same indicator using all the values observed during the months of recession. For an ideal business cycle indicator, the two histograms would be completely separate (that is, there would be no overlapping between them). For a random business cycle indicator, the two histograms would be identical. The mathematical approach to measuring the amount of overlap for these two histograms as it approximately relates to constructing the area under the curve is to add up the heights of the two histograms for all values of the indicator they have in common and subtract this total from 1.
13 We continue to use Kalman smoothed estimates of the new index for our in-sample evaluation framework. A real-time test of predictive ability would instead involve the use of the one-sided Kalman filtered estimates in addition to a reestimation of the model using only the available data at the time of prediction—for example, only the data updates available in late February 2001 for the initial March 5, 2001, release of the CFNAI. Such “vintage,” or unrevised, data does not exist for the new index at this time, but does for the CFNAI-MA3 and the ADS index. For a discussion of the real-time performance of the CFNAI-MA3, see Brave and Butters (2010).
14 The threshold values in panel A of figure 7 are in standard deviation units from a mean of zero for the new index. The equivalent values in monthly annualized real GDP growth units $\left( {{c}^{*}} \right)$ are shown in panels A and B of figure B3 in box 3.
15 For additional reference, see box 2 and figure B2, which plots the time series for each Conference Board index against our new activity index and the two business cycle components that form it.
16 The upper and lower thresholds in panel A of figure 10 assign a relative weight of 4 and 5 to the ratio of true positives to false positives, as described in box 3, based on the state of the inflation cycle 12 months hence. The relative weights were chosen to broadly match the threshold values for the new index with those of the CFNAI-MA3.
17 The threshold values in panel A of figure 10 are in standard deviation units from a mean of zero for the leading component of the new activity index. The equivalent values in monthly annualized real GDP growth units $\left( {{c}^{*}} \right)$ are shown in panels C and D of figure B3 in box 3.
Box 1. From principal components to collapsed dynamic factor analysis
Here, we explain the mathematics behind principal components analysis and its relationship to collapsed dynamic factor analysis. Let ${{x}_{t}}$ denote the $N\times 1$ column vector of $N$ data series at time $t$. The first step is to form the $N\times T$ stacked matrix of data vectors $X$, where each row of this matrix contains $T$ observations normalized to have a mean of zero and a standard deviation of one.a The eigenvector–eigenvalue decomposition of the variance–covariance matrix $\frac{X{X}'}{N}$ then produces a set of time-invariant weights referenced by the $1\times N$ row vector $w$ resulting from a transformation of the eigenvector associated with the largest eigenvalue of this matrix. These weights are then used to construct a weighted average of the ${{x}_{t}}$ such that the resulting index is given by ${{I}_{t}}=w{{x}_{t}}.$
The underlying assumption about $X$ necessary to produce this variance decomposition is that it admits an approximate factor model representation. This means that it can be additively decomposed into the product of two vectors—an $N\times 1$ column vector of time-invariant factor loadings $\Gamma$ and a $1\times T$ time-varying latent factor $F$—and a normally distributed mean zero random variable $\unicode{x03B5} $ with variance–covariance matrix ${{\unicode{x03c3} }^{2}}I$:
\[X=\Gamma F+\unicode{x03B5} .\]
The estimated values of $\hat{\Gamma }$ are obtained by maximizing $\text{tr}\left[ {\Gamma }'X{X}'\Gamma \right]$ subject to a normalization constraint on $\Gamma $.b This linear optimization problem is solved by setting the estimator $\frac{{{\hat{\Gamma }}'}}{\sqrt{N}}$ equal to $w$.c In a single factor model, the estimated index, given by ${{I}_{t}}=\frac{{\hat{\Gamma }}'{{x}_{t}}}{\sqrt{N}},$ corresponds to the first principal component. As such, it is the principal component common to all $N$ data series that explains the largest amount of variation among them.
PCA is a static estimation method in that it does not separately incorporate information from both the cross section of data series and the information from across time. Dynamic factor analysis instead makes more explicit the use of the common variation in both the cross-sectional and time dimensions (Stock and Watson, 2011). To do so, it relies on signal extraction methods, such as the Kalman filter, applied to a system of equations relating the latent factor to both the cross section of data series at each point in time (a measurement, or observation, equation) and the dynamics that drive the factor’s fluctuations over time (a state equation). Mathematically, this involves specifying the following state-space representation:
\[{{x}_{t}}=\Gamma {{f}_{t}}+{{\unicode{x03B5} }_{t}},\]
\[{{f}_{t}}=A{{f}_{t-1}}+{{\unicode{x03c5} }_{t}},\]
where ${{f}_{t}}$ is the latent factor capturing a common source of variation in the $N\times 1$ column vector of indicators ${{x}_{t}}$ at each point in time $t$; $\Gamma $ is the time-invariant $N\times 1$ loadings onto the factor; and $A$ is the transition matrix describing the evolution of the latent factor from time $t-1$ to $t$.
We write the $A$ parameter of the model assuming a first-order autoregressive process (AR(1)) for the factor; but $A$ can be generalized to an arbitrary number of lags, $p$. Both ${{\unicode{x03B5} }_{t}}$ and ${{\unicode{x03c5} }_{t}}$ are assumed to be independently normally distributed mean zero random variables. Following Doz, Giannone, and Reichlin (2012), it is also standard practice to assume that $\text{Var}\left( {{\unicode{x03B5} }_{t}} \right)\text{ }=H$ (an $N\times N$ diagonal matrix) and $\text{Var}\left( {{\unicode{x03c5} }_{t}} \right)=1$.d The signal extraction methods of the Kalman filter and smoother are then capable of estimating such a model via maximum likelihood given the coefficient matrices of the measurement and state equations, that is, $\Gamma $ and $A$, and the idiosyncratic error variances along the diagonal of $H$.
The static factor model representation of PCA thus forms the measurement equation of the state-space representation of a dynamic factor model. Adding dynamics of some finite order to the factor yields its state equation. To see the relationship between the static and dynamic factor models, consider the case where the transition matrix of the state equation is the zero matrix; that is, nullify the impact of dynamics for the latent factor. Notice if we specify that the variance–covariance matrix of the measurement equation’s error term is proportional to the identity matrix, we end up with an estimate of the latent factor that is proportional to the first principal component. For this reason, PCA can be considered a special case of the dynamic factor model with a zero transition matrix and a homoskedastic idiosyncratic error structure (that is, the assumption of equal variances across idiosyncratic drivers of the underlying data series).
Collapsed dynamic factor analysis instead first applies a transformation ${{A}_{\text{L}}}$ to the measurement equation of the dynamic factor model in order to collapse its size to match the typically much smaller number of factors. Bräuning and Koopman (2014) suggest the use of the transformation ${{A}_{\text{L}}}=\frac{{{\hat{\Gamma }}'}}{\sqrt{N}},$ where $\hat{\Gamma }'$ is the PCA estimate of the factor loadings of the static factor model. Such a “collapse” of the data leads to the following transformed measurement equation:
\[x_{t}^{\text{L}}={{f}_{t}}+{{u}_{t~}},\]
where $x_{t}^{\text{L}}=\frac{{\hat{\Gamma }}'{{x}_{t}}}{\sqrt{N}}$ is the first principal component of the data and ${{u}_{t}}=\frac{{\hat{\Gamma }}'{{\unicode{x03B5} }_{t}}}{\sqrt{N}}.$ The random scalar ${{u}_{t}}$ in this context has the interpretation of a “measurement error” between the first principal component and its static factor model counterpart, where the implicit assumption maintained to derive this expression is that $\frac{{\hat{\Gamma }}'\Gamma }{N}\cong 1.$ The measurement error variance is then estimated as an additional parameter as in the classical errors-in-variables framework, where its identification is made possible by the inclusion of an additional measurement equation containing a “target” variable, ${{y}_{t}}$, which loads onto the factor but is orthogonal to ${{u}_{t}}$. In box 2, we lay out the particular collapsing strategy and target variable that we use for this purpose in constructing a new economic activity index for the United States.
a Underlying the normalization of the data is the concept of stationarity, or in this case the first and second moment restrictions that the mean and variance of each indicator do not vary over time. Each data series first receives a transformation to make it stationary prior to its normalization.
b The normalization constraint most commonly used for this purpose is $\frac{{\Gamma }'\Gamma }{N}=1.$ However, it is also possible to use the alternative normalization $\frac{{F}'F}{T}=1$ instead.
c Note that the identification of the approximate factor model is achieved only up to scale, which is set by the normalization constraint on the factor loadings or factor.
d The latter restriction acts to set the scale of the dynamic factor model just as the restriction on the scale of the factor loadings used in PCA does for the static factor model.
Box 2. Estimating the new activity index
The construction of the new economic activity index is based on a trend–cycle decomposition of monthly U.S. real GDP growth. In matrix form, this decomposition is given by
\[{{y}_{t}}=\left[ \begin{matrix} 1 & 1 \\ \end{matrix} \right]\left[ \begin{matrix} {{\unicode{x03BC}}_{t}} \\ {{f}_{t}} \\ \end{matrix} \right]+{{\unicode{x03B1}}_{t}}+{{\unicode{x03B7}}_{t}},\]
\[{{x}_{t}}=\left[ \begin{matrix} \textbf{1} & \Gamma \\ \end{matrix} \right]\left[ \begin{matrix} {{\unicode{x03BC}}_{t}} \\ {{f}_{t}} \\ \end{matrix} \right]+{{\unicode{x03B5}}_{t}},\]
where ${{y}_{t}}$ is latent monthly annualized log real GDP growth and ${{x}_{t}}$ is our stationary, demeaned, and standardized panel of 500 monthly time series for U.S. real economic activity as described in table A1 of the separate appendix.e Both ${{y}_{t}}$ and ${{x}_{t}}$ are assumed to depend on two common factors, ${{\unicode{x03BC} }_{t}}$ and ${{f}_{t}}$. The sum of these two factors, ${{c}_{t}}\equiv {{\unicode{x03BC}}_{t}}+{{f}_{t}}$, defines the new index as the cycle component of real GDP growth. The trend rate of growth around which the new index is benchmarked is given by the latent variable ${{\unicode{x03B1} }_{t}}$ . The remaining irregular components of our decomposition, ${{\unicode{x03B7} }_{t}}$ and ${{\unicode{x03B5} }_{t}}$, are orthogonal identically normally distributed mean zero random variables.
To collapse the panel of 500 monthly time series, we premultiply it as shown here:
\[\left[ \begin{matrix} {{l}'} \\ {{\hat{\Gamma }}'} \\ \end{matrix} \right]{{x}_{t}}=\left[ \begin{matrix} {{l}'} \\ {{\hat{\Gamma }}'} \\ \end{matrix} \right]\left[ \begin{matrix} \textbf{1} & \Gamma \\ \end{matrix} \right]\left[ \begin{matrix} {{\unicode{x03BC}}_{t}} \\ {{f}_{t}} \\ \end{matrix} \right]+\left[ \begin{matrix} {{l}'} \\ {{\hat{\Gamma }}'} \\ \end{matrix} \right]{{\unicode{x03B5}}_{t}},\]
where $l$ and $\hat{\Gamma }$ are the factor loadings obtained from restricted principal components analysis (RPCA) of ${{x}_{t}}$ using the expectation-maximization algorithm described in Reis and Watson (2010).f By construction, this algorithm imposes the following scale and sign normalizations on the elements of our collapse vector, ${l}'\textbf{1}=1$ and ${\hat{\Gamma }}'\textbf{1}=0$. Given that the variables in ${{x}_{t}}$ have all been demeaned and standardized, ${{\bar{x}}_{t}}\equiv {l}'{{x}_{t}}$ can be interpreted as the cross-sectional weighted average of ${{x}_{t}}$, with the weights equal to the inverse of their standard deviations. Similarly, ${{\hat{f}}_{t}}\equiv \hat{{\Gamma }}'{{x}_{t}}$ is also a cross-sectional weighted average of ${{x}_{t}}$, but with weights that maximize the variation explained by ${{\hat{f}}_{t}}$ beyond that explained by ${{\bar{x}}_{t}}$.
We set ${\hat{\Gamma }}'\Gamma =1$, following the precedent of Bräuning and Koopman (2014), and let ${l}'\Gamma =\unicode{x03b3}$ (with $\unicode{x03b3} $ being a scalar parameter) to obtain the collapsed measurement equation
\[\left[ \begin{matrix} {{{\bar{x}}}_{t}} \\ {{\hat{f}}_{t}} \\ \end{matrix} \right]=\left[ \begin{matrix} 1 & \unicode{x03b3} \\ 0 & 1 \\ \end{matrix} \right]\left[ \begin{matrix} {{\unicode{x03BC}}_{t}} \\ {{f}_{t}} \\ \end{matrix} \right]+\left[ \begin{matrix} {{{\bar{\unicode{x03B5}}}}_{t}} \\ {{{\hat{\unicode{x03B5}}}}_{t}} \\ \end{matrix} \right],\]
where ${{\bar{x}}_{t}}$ and ${{\hat{f}}_{t}}$ are the first two restricted principal components of ${{x}_{t}}$. The classical measurement errors, ${{\bar{\unicode{x03B5}}}_{t}}$ and ${{{\hat{\unicode{x03B5}}}}_{t}}$, for the restricted principal components and the model’s underlying factors then correct for potential bias in the estimation of the factor loadings by RPCA arising from the presence of weak factors in our panel of time series, as described in the main text. Real GDP growth then acts as our target variable, or instrument, which corrects for this bias given that both measurement errors remain orthogonal to ${{\unicode{x03B1}}_{t}}$ and ${{\unicode{x03B7}}_{t}}$ by construction. Furthermore, given our sign normalization ${\hat{\Gamma }}'\textbf{1}=0$, it will necessarily be the case that $\text{Cov}({{\bar{\unicode{x03B5}}}_{t}},{{{\hat{\unicode{x03B5}}}}_{t}})=0$ as well.
In state-space form, our complete collapsed dynamic factor model can then be written as
\[\left[ \begin{matrix} {{y}_{t}} \\ {{{\bar{x}}}_{t}} \\ {{\hat{f}}_{t}} \\ \end{matrix} \right]=\left[ \begin{matrix} 1 & 1 & 1 & 1 \\ 1 & \unicode{x03b3} & 0 & 0 \\ 0 & 1 & 0 & 0 \\ \end{matrix} \right]\left[ \begin{matrix} {{\unicode{x03BC}}_{t}} \\ {{f}_{t}} \\ {{\unicode{x03B1}}_{t}} \\ {{\unicode{x03B7}}_{t}} \\ \end{matrix} \right]+\left[ \begin{matrix} 0 \\ {{\bar{\unicode{x03B5}}}_{t}} \\ {{{\hat{\unicode{x03B5}}}}_{t}} \\ \end{matrix} \right],\]
\[\left[ \begin{matrix} {{\unicode{x03BC}}_{t}} \\ {{f}_{t}} \\ {{\unicode{x03B1}}_{t}} \\ {{\unicode{x03B7}}_{t}} \\ \end{matrix} \right]=\left[ \begin{matrix} \unicode{x03c1} & 0 & 0 & 0 \\ 0 & \unicode{x03c6} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{matrix} \right]\left[ \begin{matrix} {{\unicode{x03BC}}_{t-1}} \\ {{f}_{t-1}} \\ {{\unicode{x03B1}}_{t-1}} \\ {{\unicode{x03B7}}_{t-1}} \\ \end{matrix} \right]+\left[ \begin{matrix} {{\unicode{x03c5}}_{t}} \\ {{\unicode{x03be}}_{t}} \\ {{\unicode{x03bd}}_{t}} \\ {{\unicode{x03B7}}_{t}} \\ \end{matrix} \right],\]
with error covariance matrices,
\[H=\left[ \begin{matrix} 0 & 0 & 0 \\ 0 & \unicode{x03c3}^{2}_{{\bar{\unicode{x03B5}}}} & 0 \\ 0 & 0 & \unicode{x03c3}^{2}_{{\hat{\unicode{x03B5}}}} \\ \end{matrix} \right],Q=\left[ \begin{matrix} \unicode{x03c3}^{2}_{\unicode{x03c5}} & 0 & 0 & 0 \\ 0 & \unicode{x03c3}^{2}_{\unicode{x03be}} & 0 & 0 \\ 0 & 0 & \unicode{x03c3}^{2}_{\unicode{x03bd}} & 0 \\ 0 & 0 & 0 & \unicode{x03c3}^{2}_{\unicode{x03B7}} \\ \end{matrix} \right].\]
To separately identify the common factors ${{\unicode{x03BC}}_{t}}$ and ${{f}_{t}}$, we restrict their joint dynamics by specifying that each follows a stationary univariate first-order autoregression $\left( \left| \unicode{x03c1} \right|<1\ \text{and}\="" \left|="" \unicode{x03c6}=""><1 \right)$="" and="" additionally="" requiring="" that="" $\text{cov}({{\unicode{x03c5}}_{t}},{{\unicode{x03be}}_{t}})="0$." trend="" real="" gdp="" growth="" is="" assumed="" to="" follow="" a="" random="" walk,="" where="" we="" parameterize="" $\unicode{x03c3}^{2}_{\unicode{x03bd}}="\unicode{x03c4}\times" \unicode{x03c3}^{2}_{\unicode{x03b7}}$,="" with="" $\unicode{x03c4}="" $="" preset="" using="" the="" stock="" and="" watson="" (1998)="" median="" unbiased="" estimation="" method="" to="" avoid="" the="" pileup="" problem="" in="" the="" estimation="" of="">
Next, we specify an additional measurement equation constraining the monthly latent states to match the quarterly real GDP data by incorporating additional state variables called “accumulators” (Harvey, 1989); these variables act to recursively impose the temporal aggregation properties of the observed data. For the annualized (log) growth rate of quarterly real GDP, ${{y}_{3t}}$, the accumulator takes the following deterministic form of “triangle averaging,”
\[{{y}_{3t}}=\frac{1}{3}{{y}_{t}}+\frac{2}{3}{{y}_{t-1}}+{{y}_{t-2}}+\frac{2}{3}{{y}_{t-3}}+\frac{1}{3}{{y}_{t-4}},\]
where we assume that we only observe ${{y}_{3t}}$ in the third month of each quarter.g
The resulting mixed-frequency dynamic factor model is estimated by maximum likelihood as described in Durbin and Koopman (2012) with a MATLAB toolbox detailed in Brave, Butters, and Kelley (2018). Figure B1 shows the Kalman smoothed estimates of the components that sum to form monthly real GDP growth. The cycle components ${{\unicode{x03BC}}_{t}}$ and ${{f}_{t}}$ explain roughly 48 percent of real GDP growth’s variation; variation over time in the trend ${{\unicode{x03B1}}_{t}}$ accounts for 5 percent of real GDP growth’s variation; and the irregular component ${{\unicode{x03B7}}_{t}}$ explains the rest.
Figure B1. Trend–cycle decomposition of monthly U.S. real GDP growth
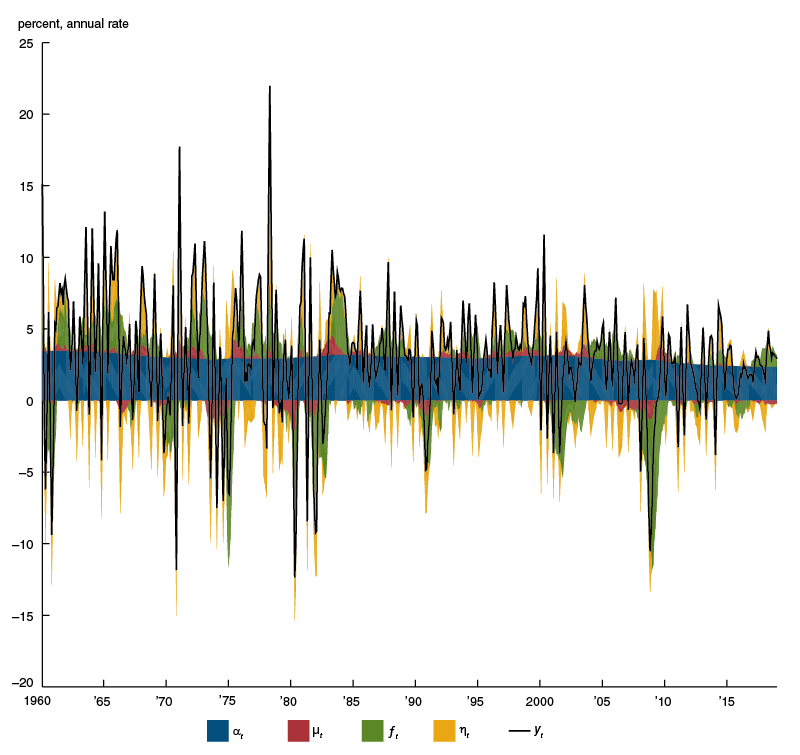
Source: Authors’ calculations based on data from Haver Analytics.
To gain further insights about what distinguishes the cycle components ${{\unicode{x03BC}}_{t}}$ and ${{f}_{t}}$ from each other, we plot in figure B2 each component individually (panels B and C) as well as their sum ${{c}_{t}}$ (panel A) against the Conference Board’s Leading, Lagging, and Coincident Economic Indexes for the U.S., respectively. The shading in the figure corresponds to U.S. recessions as determined by the National Bureau of Economic Research, and the correlation coefficient for the indexes is reported in the top right of each panel. It is readily apparent from panel A that our new activity index $({{c}_{t}})$ is highly correlated with the Conference Board Coincident Economic Index for the U.S., consistent with our interpretation of ${{c}_{t}}$ . It is also easily seen from panel B that what largely distinguishes ${{\unicode{x03BC}}_{t}}$ from ${{f}_{t}}$ is that it is a leading indicator of the cycle, evidenced in its strong correlation with the Conference Board Leading Economic Index for the U.S. That said, ${{f}_{t}}$ does not display the archetypical properties of a lagging indicator, evidenced by its very low correlation with the Conference Board Lagging Economic Index for the U.S. In fact, it much more closely resembles a coincident indicator. These properties lead us to refer to ${{\unicode{x03BC}}_{t}}$ as the leading component of the new index and ${{f}_{t}}$ as the slightly lagging component of the new index for reasons that are further discussed in the main text.
Figure B2. New activity index versus Conference Board indexes
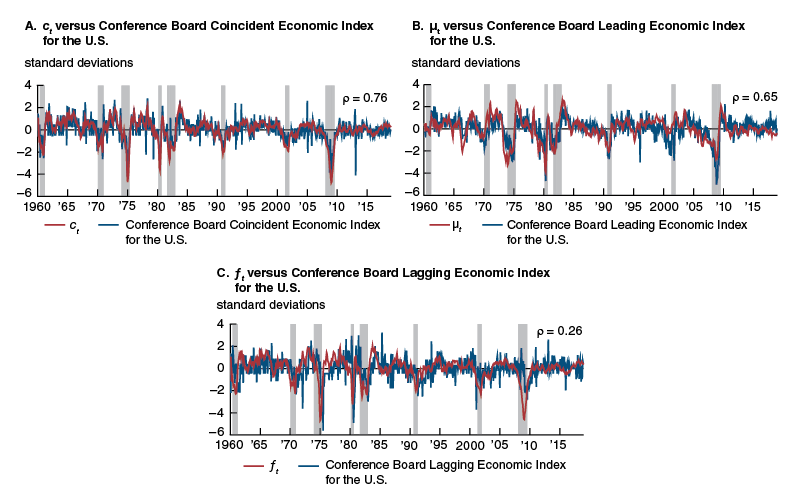
Source: Authors’ calculations based on data from Haver Analytics.
The lead–lag properties of our cycle components ${{\unicode{x03BC}}_{t}}$ and ${{f}_{t}}$ are themselves a reflection of subtle differences in the behavior over the cycle of the restricted principal components ${{\bar{x}}_{t}}$ and ${{\hat{f}}_{t}}$, and are what make it possible to separately identify two factors in our model. These differences are based on the cyclical properties of our panel of 500 macroeconomic time series, which contains clusters of leading, lagging, and coincident indicators. Our work suggests that one factor is not enough to accurately capture these distinctions in U.S. data and is in line with D’Agostino et al. (2016), who also find that accurately capturing the business cycle with dynamic factor methods requires careful treatment of the lead–lag properties of the underlying data.
e Available online. For the purpose of estimation, we also demean and standardize real GDP growth as well. After the estimation, the mean is then added back into the trend component and all four components are scaled up by the standard deviation.
f To compensate for the fact that not all of our time series are the same length, we use the EM algorithm of Stock and Watson (2002a, 2002b) to extract the restricted principal components in the presence of incomplete data. In addition, because both RPCA and PCA are only identified up to a sign flip, we impose sign restrictions on the panel of time series and the restricted principal components to ensure a positive correlation with real GDP growth.
g Implicitly, this representation requires that the observed lower-frequency time series (in this case, quarterly real GDP) is well approximated by the geometric mean—as opposed to the more traditional arithmetic mean—of the underlying higher-frequency time series (for example, monthly real GDP). For this application, this representation has been shown to be a reasonable approximation and further facilitates the use of a linear state-space system (Mariano and Murasawa, 2003, 2010).
Box 3. Receiver operating characteristics analysis
Receiver operating characteristics analysis requires that we categorize each observation of an index as falling within a recession or expansion. Following the dating conventions for U.S. business cycles of the National Bureau of Economic Research,h we then need to construct the conditional probabilities:
\[\text{TP}\left( c \right)=\text{Prob}\left[ {{I}_{t}}\ge c\text{ }\text{ }\!\!|\!\!\text{ }\text{ }{{S}_{t}}=1 \right],\]
\[\text{FP}\left( c \right)=\text{Prob}\left[ {{I}_{t}}\ge c\text{ }\text{ }\!\!|\!\!\text{ }\text{ }{{S}_{t}}=0 \right],\]
with ${{S}_{t}}\in \left\{ 0,\text{ }1 \right\}$ indicating recessions and expansions, respectively. $\text{TP}\left( c \right)$ is typically referred to as the true positive rate and $\text{FP}\left( c \right)$ is known as the false positive rate for an index ${{I}_{t}}$ and particular observed value $c$. The relationship between the two is described by the ROC curve. With the Cartesian convention, this curve is given by
\[\left\{ \text{ROC}\left( r \right),r \right\}_{r=0}^{1},\]
where $~\text{ROC}\left( r \right)=\text{TP}\left( c \right)$ and $r=\text{FP}\left( c \right)$. In the rest of this box, we describe how to construct this curve.
First, we find the fraction of observations that the NBER has classified as expansions and then as recessions. These fractions are the unconditional probabilities associated with expansions and recessions. To obtain conditional probabilities, we use the following algorithm: For each value between the minimum and maximum observations of an index, we find the fraction of observations where that value and all subsequently higher values fall in months outside of recessions. We then do the same to find the fraction of observations that fall in months during recessions. These two fractions are equivalent to the true positive and false positive rates that we just defined. By plotting the true positive and false positive rates against each other for every historical value of an index, we produce a nonparametric estimate of its ROC curve.
Berge and Jordà (2011) show that by calculating the area under this curve, we arrive at an estimate of the ability of the index to delineate recessions from expansions. As the area under the curve approaches 1, the more predictive it is.i For example, an AUC value of 0.99 indicates that only 1 percent of the observations of an index are consistent with both recessions and expansions in the United States since 1960. It is on this basis that one can state that such an index is 99 percent accurate in identifying business cycles. Its statistical significance is then judged relative to the area under the line from the origin extending at a 45-degree angle corresponding to a benchmark where any given observation of the index is equally likely to occur during an expansion or recession.j It is also possible to compare the areas under two different ROC curves in order to distinguish the statistical significance of differences in their predictive abilities.
As an example, panel A of figure B3 displays the ROC curve for the new activity index and recessions, along with a line from the origin extending at a 45-degree angle. By construction, this line has an AUC value equal to 0.5. The more the ROC curve deviates in total above this 45-degree line, the higher an index’s AUC value will be. In addition, for an index’s AUC value to exceed 0.5, it must have a slope greater than 1 at some point on the ROC curve such that, for a given increase in the true positive rate, the associated increase in the false positive rate is smaller. The circled red dot on the curve marks the point at which it is no longer possible to increase the true positive rate without producing more false positives than are consistent with the observed relative frequency of expansions and recessions.
Figure B3. ROC curves for U.S. business and inflation cycles
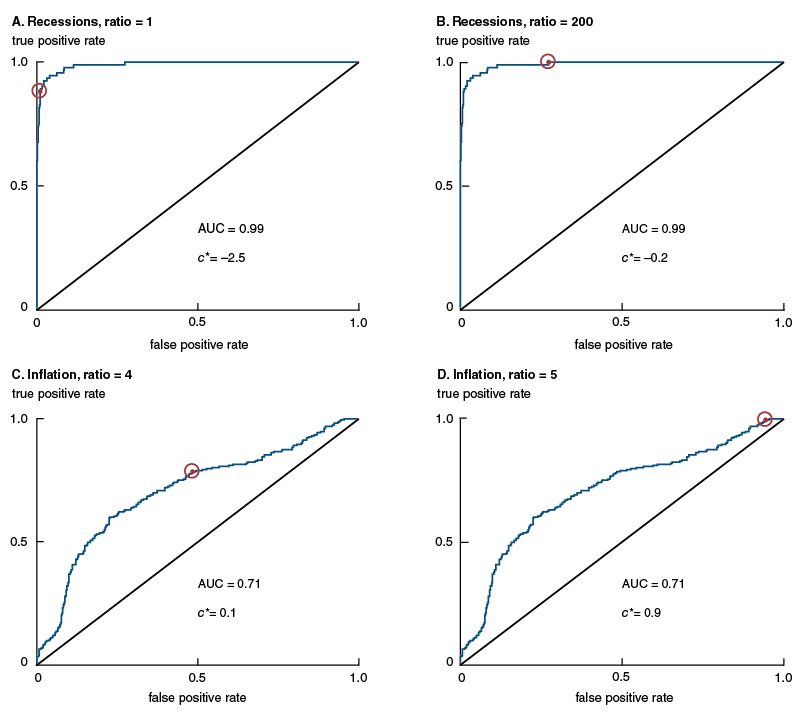
Source: Authors’ calculations based on data from Haver Analytics.
Baker and Kramer (2007) show that the point on the curve in panel A of figure B3 denoted by the circled red dot meets the decision-theoretic criteria for a threshold rule $\left( {{c}^{*}} \right)$ that equally penalizes type I (false positive) and type II (false negative) classification errors for recessions and expansions. To see this, consider the following utility function:
\[U=~{{U}_{11}}\text{ROC}\left( r \right)\unicode{x03c0} +{{U}_{01}}\left( 1-\text{ROC}\left( r \right) \right)\unicode{x03c0} +{{U}_{10}}r\left( 1-\unicode{x03c0} \right)+{{U}_{00}}\left( 1-r \right)\left( 1-\unicode{x03c0} \right),\]
where ${{U}_{ij}}$ is the utility (or disutility) associated with the prediction $i$ given that the true state of the business cycle, ${{S}_{t}}$, is $j$, with $\left\{ i,j \right\}\in \left\{ 0,\text{ }1 \right\}$, and where $\unicode{x03c0} $ is the unconditional probability of a recession. Utility maximization implies the following first-order condition determining ${{c}^{*}}$:
\[\frac{\partial \text{ROC}}{\partial r}=\frac{{{U}_{00}}-{{U}_{10}}}{{{U}_{11}}-{{U}_{01}}}\frac{1-\unicode{x03c0}}{\unicode{x03c0}}.\]
This threshold equates the slope of the ROC curve to the ratio of the unconditional probabilities of expansion and recession, $\frac{1-\unicode{x03c0}}{\unicode{x03c0}}$, weighted by the ratio of utilities, $\frac{{{U}_{00}}-{{U}_{10}}}{{{U}_{11}}-{{U}_{01}}}$.
Equally weighting the net benefit of a type I versus a type II error relative to correctly predicting the true state corresponds with setting this ratio of utilities to 1. Increasing this ratio above 1 moves the red dot upward along the curve, in essence accepting additional false positives in an effort to increase the true positive rate. This can be seen in panel B of figure B3, in the circled red dot corresponding to the higher threshold used to capture the absence of any false negative signals of the new index for recessions (as described in the main text). Panels C and D of figure B3 contain threshold values for the U.S. inflation cycles described in box 4 at a lead of 12 months for the leading component of the new index, with the ratio of utilities set to 4 and 5, respectively. All of the threshold values in figure B3 are presented in annualized (log) percent changes.
i This assumes that the index is procyclical or, in other words, is positively correlated with expansions. All of the indexes we examine meet this criteria. For countercyclical indexes, improvements in predictive ability correspond to the area under the curve approaching zero instead.
j The procedure for evaluating statistical significance is described in DeLong, DeLong, and Clarke-Pearson (1988).
Box 4. Inflation cycle dating algorithm
Here we describe a method for identifying episodes of sustained increasing inflation, or what we refer to as inflation cycles in the main text. We consider two measures of core consumer prices (which exclude volatile food and energy prices): the core Price Index for Personal Consumption Expenditures (PCE) from the U.S. Bureau of Economic Analysis and the core Consumer Price Index (CPI) from the U.S. Bureau of Labor Statistics. Monthly inflation rates over a 12-month period are computed for each inflation series. There are then five steps for establishing an inflation cycle.
- Starting in January 1960, determine when each inflation measure reaches a minimum.
- Then, determine the subsequent dates when each inflation measure has risen by 0.75 percentage points from its minimum. While only one series rising 0.75 percentage points can trigger an inflation cycle, in order for this date to be considered the start of a cycle, the other series must be moving in an upward direction; that is, we require that there must be “co-movement.”k These dates constitute the start of the inflation cycle.
- Determine the dates when each inflation measure has reached its maximum value and then begins a “reasonably” continuous decline, which we define as each inflation measure having fallen by 0.75 percentage points from its maximum value during the cycle. These dates are then taken to be the end of the inflation cycle.
- Only begin a cycle when both inflation measures are above 2 percent (that is, at least one inflation measure must reach at least 2.75 percent during the cycle).
- Date the overall inflation cycle by selecting the earliest start date and latest end date.
Our five inflation cycles occur during the following periods: June 1966–October 1971, May 1973–May 1975, June 1977–June 1981, December 1987–July 1991, and October 2004–November 2008. Criteria 2 through 4 have real effects on determining these periods. For instance, they rule out a brief period during 1984 when core CPI was rising while core PCE was not; the early 2000s when core PCE barely peaked above 2 percent; and several instances in the past decade when both core inflation measures were below 2 percent.
k We operationalize this constraint by imposing that if the three-month change in the 12-month inflation rate for either series is less than 0.125 percentage points at the candidate month, that date is rejected as a possible inflation cycle start date.
REFERENCES
Aruoba, S. B., F. X. Diebold, and C. Scotti, 2009, “Real-time measurement of business conditions,” Journal of Business & Economic Statistics, Vol. 27, No. 4, October, pp. 417–427. Crossref
Bai, J., and S. Ng, 2002, “Determining the number of factors in approximate factor models,” Econometrica, Vol. 70, No. 1, January, pp. 191–221. Crossref
Baker, S. G., and B. S. Kramer, 2007, “Peirce, Youden, and receiver operating characteristic curves,” American Statistician, Vol. 61, No. 4, November, pp. 343–346. Crossref
Bańbura, M., and M. Modugno, 2014, “Maximum likelihood estimation of factor models on datasets with arbitrary pattern of missing data,” Journal of Applied Econometrics, Vol. 29, No. 1, January/February, pp. 133–160. Crossref
Berge, T. J., and Ò. Jordà, 2011, “Evaluating the classification of economic activity into recessions and expansions,” American Economic Journal: Macroeconomics, Vol. 3, No. 2, April, pp. 246–277. Crossref
Bok, B., D. Caratelli, D. Giannone, A. Sbordone, and A. Tambalotti, 2017, “Macroeconomic nowcasting and forecasting with big data,” Federal Reserve Bank of New York, staff report, No. 830, November, available online.
Bräuning, F., and S. J. Koopman, 2014, “Forecasting macroeconomic variables using collapsed dynamic factor analysis,” International Journal of Forecasting, Vol. 30, No. 3, July–September, pp. 572–584. Crossref
Brave, S. A., 2009, “The Chicago Fed National Activity Index and business cycles,” Chicago Fed Letter, Federal Reserve Bank of Chicago, No. 268, November, available online.
Brave, S. A., and R. A. Butters, 2014, “Nowcasting using the Chicago Fed National Activity Index,” Economic Perspectives, Federal Reserve Bank of Chicago, Vol. 38, First Quarter, pp. 19–37, available online.
Brave, S. A., and R. A. Butters, 2013, “Estimating the trend rate of economic growth using the CFNAI,” Chicago Fed Letter, Federal Reserve Bank of Chicago, No. 311, June, available online.
Brave, S. A., and R. A. Butters, 2010, “Chicago Fed National Activity Index turns ten—Analyzing its first decade of performance,” Chicago Fed Letter, Federal Reserve Bank of Chicago, No. 273, April, available online.
Brave, S. A., R. A. Butters, and D. Kelley, 2019, “Multi-sector business cycle accounting in a data-rich environment,” Federal Reserve Bank of Chicago and Indiana University, Kelley School of Business, unpublished manuscript, February, available online.
Brave, S. A., R. A. Butters, and D. Kelley, 2018, “A practitioner’s guide and MATLAB toolbox for mixed frequency state space models,” Federal Reserve Bank of Chicago and Indiana University, Kelley School of Business, unpublished manuscript, November, available online.
Brave, S. A., and M. Lichtenstein, 2012, “A different way to review the Chicago Fed National Activity Index,” Chicago Fed Letter, Federal Reserve Bank of Chicago, No. 298, May, available online.
Chamberlain, G., and M. Rothschild, 1983, “Arbitrage, factor structure, and mean-variance analysis on large asset markets,” Econometrica, Vol. 51, No. 5, September, pp. 1281–1304. Crossref
Chudik, A., M. H. Pesaran, and E. Tosetti, 2011, “Weak and strong cross-section dependence and estimation of large panels,” Econometrics Journal, Vol. 14, No. 1, pp. C45–C90. Crossref
D’Agostino, A., D. Giannone, M. Lenza, and M. Modugno, 2016, “Nowcasting business cycles: A Bayesian approach to dynamic heterogeneous factor models,” in Dynamic Factor Models, E. Hillebrand and S. J. Koopman (eds.), Advances in Econometrics, Vol. 35, Bingley, UK: Emerald Group, pp. 569–594. Crossref
DeLong, E. R., D. M. DeLong, and D. L. Clarke-Pearson, 1988, “Comparing the areas under two or more correlated receiver operating characteristic curves: A nonparametric approach,” Biometrics, Vol. 44, No. 3, September, pp. 837–845. Crossref
Doz, C., D. Giannone, and L. Reichlin, 2012, “A quasi-maximum likelihood approach for large, approximate dynamic factor models,” Review of Economics and Statistics, Vol. 94, No. 4, November, pp. 1014–1024. Crossref
Durbin, J., and S. J. Koopman, 2012, Time Series Analysis by State Space Methods, 2nd ed., Oxford Statistical Science Series, Vol. 38, Oxford, UK: Oxford University Press. Crossref
Evans, C. L., C. T. Liu, and G. Pham-Kanter, 2002, “The 2001 recession and the Chicago Fed National Activity Index: Identifying business cycle turning points,” Economic Perspectives, Federal Reserve Bank of Chicago, Vol. 26, Third Quarter, pp. 26–43, available online.
Exterkate, P., D. van Dijk, C. Heij, and P. J. F. Groenen, 2013, “Forecasting the yield curve in a data-rich environment using the factor-augmented Nelson–Siegel model,” Journal of Forecasting, Vol. 32, No. 3, April, pp. 193–214. Crossref
Fisher, J. D. M., 2000, “Forecasting inflation with a lot of data,” Chicago Fed Letter, Federal Reserve Bank of Chicago, No. 151, March, available online.
Geweke, J., 1977, “The dynamic factor analysis of economic time-series models,” in Latent Variables in Socio-Economic Models, D. J. Aigner and A. S. Goldberger (eds.), Amsterdam: North-Holland, pp. 365–383.
Giannone, D., M. Lenza, and G. E. Primiceri, 2018, “Economic predictions with big data: The illusion of sparsity,” Federal Reserve Bank of New York, staff report, No. 847, April, available online.
Giannone, D., L. Reichlin, and D. Small, 2008, “Nowcasting: The real-time informational content of macroeconomic data,” Journal of Monetary Economics, Vol. 55, No. 4, May, pp. 665–676. Crossref
Groen, J. J. J., and G. Kapetanios, 2016, “Revisiting useful approaches to data-rich macroeconomic forecasting,” Computational Statistics & Data Analysis, Vol. 100, No. C, August, pp. 221–239. Crossref
Harvey, A. C., 1989, Forecasting, Structural Time Series Models and the Kalman Filter, Cambridge, UK: Cambridge University Press.
Higgins, P., 2014, “GDPNow: A model for GDP ‘nowcasting,’” Federal Reserve Bank of Atlanta, working paper, No. 2014-7, July, available online.
Mariano, R. S., and Y. Murasawa, 2010, “A coincident index, common factors, and monthly real GDP,” Oxford Bulletin of Economics and Statistics, Vol. 72, No. 1, February, pp. 27–46. Crossref
Mariano, R. S., and Y. Murasawa, 2003, “A new coincident index of business cycles based on monthly and quarterly series,” Journal of Applied Econometrics, Vol. 18, No. 4, July/August, pp. 427–443. Crossref
McCracken, M. W., and S. Ng, 2016, “FRED-MD: A monthly database for macroeconomic research,” Journal of Business & Economic Statistics, Vol. 34, No. 4, October, pp. 574–589. Crossref
Mitchell, J., 2014, “Discussion of ‘Forecasting macroeconomic variables using collapsed dynamic factor analysis’ by Falk Bräuning and Siem Jan Koopman,” International Journal of Forecasting, Vol. 30, No. 3, July–September, pp. 585–588. Crossref
Reis, R., and M. W. Watson, 2010, “Relative goods’ prices, pure inflation, and the Phillips correlation,” American Economic Journal: Macroeconomics, Vol. 2, No. 3, July, pp. 128–157. Crossref
Sargent, T. J., and C. A. Sims, 1977, “Business cycle modeling without pretending to have too much a priori economic theory,” Federal Reserve Bank of Minneapolis, working paper, No. 55, revised January 1977, available online.
Stock, J. H., and M. W. Watson, 2011, “Dynamic factor models,” in Oxford Handbook of Economic Forecasting, M. P. Clements and D. F. Hendry (eds.), Oxford, UK: Oxford University Press. Crossref
Stock, J. H., and M. W. Watson, 2002a, “Forecasting using principal components from a large number of predictors,” Journal of the American Statistical Association, Vol. 97, No. 460, December, pp. 1167–1179. Crossref
Stock, J. H., and M. W. Watson, 2002b, “Macroeconomic forecasting using diffusion indexes,” Journal of Business & Economic Statistics, Vol. 20, No. 2, April, pp. 147–162. Crossref
Stock, J. H., and M. W. Watson, 1999, “Forecasting inflation,” Journal of Monetary Economics, Vol. 44, No. 2, October, pp. 293–335. Crossref
Stock, J. H., and M. W. Watson, 1998, “Median unbiased estimation of coefficient variance in a time-varying parameter model,” Journal of the American Statistical Association, Vol. 93, No. 441, March, pp. 349–358. Crossref










